We have a first order kinetics.
Let's call:
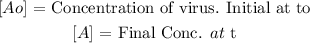
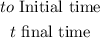
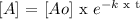
That is the formula to calculate the concentration of the virus
You can have it from this:
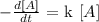
we don't have the "k" specific velocity constant
Half-life is when (A) = (Ao)/2
We have t=4.5 h ar 29.6%
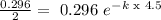
Then k= 0.15 1/h
At first order, half-time doesn't depend on Concentration
So, the time it is going to be the same:

Then the half-time will be 4.5 h.