a) We have to write a parallel line to x + 6 = 0 that passes through (-1,4).
Parallel lines always have the same slope.
In this case, this is a vertical line defined as:
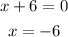
NOTE: vertical lines have undefined slopes, as they approach infinite when tried to calculate them.
Then, we have to find the vertical line that passes through (-1,4).
If (-1,4) is partof the line, then x has to be equal to -1.
As x takes only one value for a vertical line, then we can define the line as x = -1 or x + 1 = 0, which is equivalent.
b) We have to find the line that passes through (-1,4) that is perpendicular to x + 6 = 0.
Perpendicular lines have slopes that are negative reciprocals with the original slope.
In this case, as the original line is vertical (with an undefined slope), a perpendicular line will be an horizontal line (with slope m = 0).
Horizontal lines can be expressed as y = k, where k is a constant.
In this case, it has to pass through (-1,4). As y has to be equal to 4 at that point, it will be equal to 4 for all the remaining points.
Then, we can write the equation as:
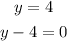
Answer:
a) x + 1 = 0
b) y - 4 = 0