To answer this question, we need to identify the formula for the line equation in the graph.
We can see that if we take two points from the graph, we have:
(0, 0)
(1, 1)
Then, to find the equation for this line, we need to find the slope of the line first:
(0, 0) ---> x1 = 0, y1 = 0
(1, 1) ---> x2 = 1, y2 = 1
The slope is:
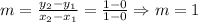
Applying the point-slope form of the line, we have:
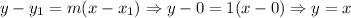
Then, the function is y = x (as we can check from the graph).
Then, we have that:
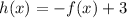
And

Therefore
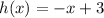
Thus, we need to graph this line using the previous equation. We need to find the x-intercept for the line (the value of x when y = 0), and the y-intercept for the line (the value of y when x = 0). Then, we have:

Then, the x-intercept is (3, 0).
And the y-intercept is (x = 0):
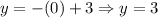
Hence, the y-intercept is (0, 3).
Therefore, if we put these two points on a graph (3, 0) and (0, 3), the graph will be:
We can see that the line has a different slope, and we can see that the y-intercept is 3, which corresponds with the new function.