Question

Graph the inequality in a coordinate plane. Label Axis2x - y >| -4

Answer 1

We need to graph the following inequality:

`2x-y\ge-4`

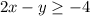
We first need to find the line that is associated with this inequality. To do that we will change it to be an equation and organize it so that the "y" will be on the left side alone. We have:

`\begin{gathered} 2x-y=-4 \\ -y=-2x-4 \\ y=2x+4 \end{gathered}`

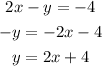
We now need to graph this line. For that we need to determine one point that belongs to it. We will choose x= 1 and calculate y.

`y=2\cdot1+4=6`

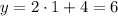
So the point is (1,6). We know that the line crosses the y-axis at 4, because the expression is in the slope-intercepet form. So we can graph this line.

We now need to find which side of the line corresponds to the inequation.

`\begin{gathered} 2x-y\ge-4 \\ -y\ge-2x-4 \\ y\leq2x+4 \end{gathered}`

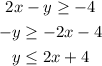
Since the signal became less equal to, then the side that we want is below the line. The final graph is shown below: