Question

in a survey, 10 people gave the following ratings for a local politician (on a scale of 0 to 100),41, 42, 43, 44, 47, 50, 52, 54, 54, 89Identify all values that are outliers.

Answer 1

To determine the outliers we need the interquartile range, defined as:

`IQR=Q_3-Q_1_{}`

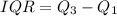
Now, we have the values ordered as:

41, 42, 43, 44, 47, 50, 52, 54, 54, 89

For this data set the median (or second quartile) is mean between the two central values 47 and 50. then we have:

`Q_2=(50+47)/(2)=48.5`

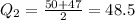
Now the set (with the median in it) is: 41, 42, 43, 44, 47, 48.5, 50, 52, 54, 54, 89

The first quartile is the median of the first half of the data in this case:

`Q_1=43`

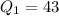
The third quartile is the median of the second half of the data i this case:

`Q_3=_{}54`

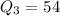
Now, the interquartile range is:

`IQR=54-43=11`

An outlier is defined as being any point of data that lies over 1.5 IQRs below the first quartile (Q1) or above the third quartile (Q3) in a data set.

Then in this case we have that the limits are:

`\begin{gathered} \text{High}=54+1.5(11)=70.5 \\ \text{Lower}=43-1.5(11)=26.5 \end{gathered}`

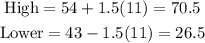
Hence any outlier in the data set have to be greater than 70.5 or smaller than 26.5. Looking at the data set we conclude that the only outlier in this data set is 89.