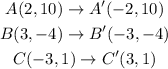Question

triangle ABV has coordinates at A(2,10), B(3,-4) and C(-3,1). write the new coordinates after the triangle is reflected over the x-axis. write the new coordinates after the triangle is reflected over the y-axis.

Answer 1

When a figure is reflected over one of the axis there is only a change on the sign of one of the coordinates.

When the reflection is done over the x-axis the transformation follows the rule

`(x,y)\rightarrow(x,-y)`

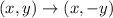
When the reflection is done over the y-axis the transformation follows the rule

`(x,y)\rightarrow(-x,y)`

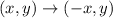
According to this if we reflect triangle ABC over the x axis then

`\begin{gathered} A(2,10)\rightarrow A^(\prime)(2,-10) \\ B(3,-4)\rightarrow B^(\prime)(3,4) \\ C(-3,1)\rightarrow C^(\prime)(-3,-1) \end{gathered}`

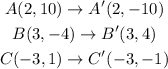
If we reflect the triangle over the y axis

`\begin{gathered} A(2,10)\rightarrow A^(\prime)(-2,10) \\ B(3,-4)\rightarrow B^(\prime)(-3,-4) \\ C(-3,1)\rightarrow C^(\prime)(3,1) \end{gathered}`