Question

Please help me with this math problem. I have to Use the quadratic formula to solve each equation.

Answer 1

You have to solve the given expression for q:

`2q^2-8=3q`

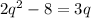
This expression has a quadratic term, which means that it is a quadratic equation. To find the value or values of q, you have to use the quadratic equation, using "q" as the variable instead of "x"

`q=(-b\pm√(b^2-4ac))/(2a)`

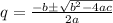
Where

a is the coefficient of the quadratic term

b is the coefficient of the q term

c is the constant

- First, zero the equation by passing 3q to the left side of the equal sign:

`\begin{gathered} 2q^2-8=3q \\ 2q^2-8-3q=3q-3q \\ 2q^2-3q-8=0 \end{gathered}`

For this equation the coefficients are:

a= 2

b= -3

c= -8

Replace them in the formula and solve:

`\begin{gathered} q=(-b\pm√(b^2-4ac))/(2a) \\ q=(-(-3)\pm√((-3)^2-4*2*(-8)))/(2*2) \\ q=(3\pm√(9+64))/(4) \\ q=(3\pm√(73))/(4) \end{gathered}`

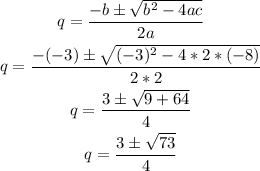
Next, to determine each possible value of q, you have to solve the sum and difference separately:

Sum

`\begin{gathered} q=(3+√(73))/(4) \\ q=2.886\cong2.9 \end{gathered}`

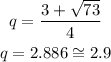
Difference

`\begin{gathered} q=(3-√(73))/(4) \\ q=-1.386\cong-1.4 \end{gathered}`

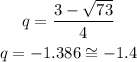
The possible solutions for the given equation are q=2.9 and q=-1.4