Question

The figure below shows a circle with a radius of 7 units from which a circle with a radius 3 units has been cut. What is the exact area of the blue region.

Answer 1

To find the blue area, you have to subtract the area of the small circle from the area of the big circle

The rule of the area of the circle is

`A=\pi(r)^2`

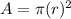
r is the radius of the circle

Then the area of blue is

`A_(blue)=A_(big)-A_(small)`

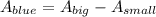
Since the radius of the small circle is 3 units and the radius of the big circle is 7 units, then

`\begin{gathered} A_(blue)=\pi(7)^2-\pi(3)^2 \\ A_(blue)=49\pi-9\pi \\ A_(blue)=40\pi \end{gathered}`

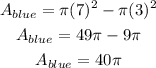
The exact area of the blue part is a 40pi square unit