Question

- 4x + y = 16– 8x + 8y = – 16Solve by graphing and whether the system is consistent or inconsistent and if it's dependent or independent

Answer 1

We are given the following equation system:

`\begin{gathered} -4x+y=16,(1) \\ -8x+8y=-16,(2) \end{gathered}`

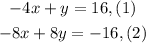
The slope-intercept form of a linear equation is the following:

`y=mx+b`

Taking equation (1):

`-4x+y=16`

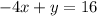
Now we solve for "y". To do that we add 4x to both sides:

`\begin{gathered} -4x+4x+y=16+4x \\ y=4x+16 \end{gathered}`

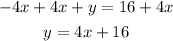
Now, taking equation (2):

`-8x+8y=-16`

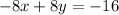
Adding 8x to both side:

`\begin{gathered} -8x+8x+8y=-16+8x \\ 8y=8x-16 \end{gathered}`

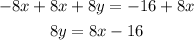
Dividing both sides by 8:

`\begin{gathered} y=(8x)/(8)-(16)/(8) \\ y=x-2 \end{gathered}`

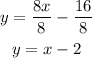
The graph of both equations are the following:

Since the graphs of each line do not have the same slope, they are a consistent system and are independent. The solution is the point where the two lines intercept, that is (x,y) = (-6,-8).