Given the following equation of a quadratic function:
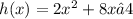
We will rewrite the quadratic function in standard form.
The general standard form will be as follows:
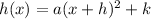
So, we will make a complete square for the given function as follows:
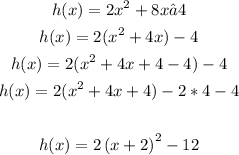
Comparing the last result to the general form:
h = -2, k = -12
So, the answer will be:
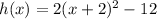
The vertex = (x,y) = (-2, -12)