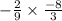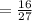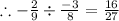To divide the given fractions, we first write each of them as improper fractions.
4 1/4 ÷ 3 1/2
Now,
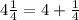
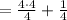
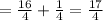
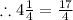
And
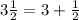
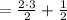
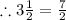
Now the division becomes
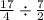
Taking the reciprocal of the left-hand fraction and converting division into multiplication gives
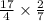
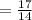
Hence,
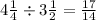
-3.5 ÷ 0.675
We first convert the decimals to fractions.
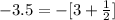
Converting this to an improper fraction gives
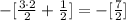
Now, 0.675 can be written as
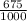
Therefore, the division can be written as
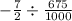
Talking the reciprocal of the right-hand fraction gives
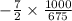
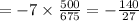
Hence,
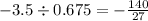
-2/9 ÷ -3/8
Taking the reciprocal of the right-hand fraction and converting the division into multiplication gives