Part (A)
The final speed of the car can be expressed as,
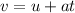
Plug in the known values,
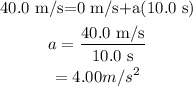
The force acting on the car can be given as,
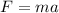
Substitute the known values,
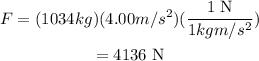
The average speed of the car can be given as,
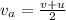
Substitute the known values,

The average mechanical output of the engine is,
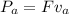
Substitute the known values,
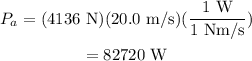
Thus, the average mechanical power output of engine is 82720 W.
Part (B)
The power generated by gasoline can be given as,

Substitute the known values,
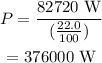
The energy generated by gasoline can be given as,

Substituting known values,
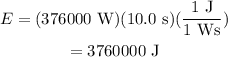
The volume consumed by gasoline can be calculated as,

Thus, the volume of gasoline consumed is 0.08 L.