Question

Suppose Set B contains 14 elements and the total number elements in either Set A or Set B is 27. If theSets A and B have 13 elements in common, how many elements are contained in set A?

Answer 1

Given:

a.) Set B contains 14 elements

b.) The total number of elements in either Set A or Set B is 27.

c.) Sets A and B have 13 elements in common.

B = 14 Elements

A ∪ B = 27

A ∩ B = 13

Let's determine how many elements are contained in set A,

`\begin{gathered} \text{ 27 = Set B + Set A} \\ \text{ 27 = 14 + Set A} \\ \text{ Set A = 27 -14} \\ \text{ Set A = 13 Elements} \end{gathered}`

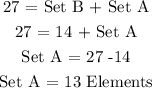
Therefore, there are 13 Elements in Set A.