Question

Can you please help solve problem correctly. My daughter did problem completing wrong. Thanks

Answer 1

Recall that to compute the equation of a line we have to have two points on the line, once we have two points we can use the following formula for the equation (unless it is a vertical line):

`y-y_1=(y_1-y_2)/(x_1-x_2)(x-x_1),`

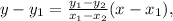
where (x₁,y₁) and (x₂,y₂) are two points on the line.

Now, notice that points (0,-1) and (3,2) are on line n, therefore its equation is:

`y-2=(2-(-1))/(3-0)(x-3)\text{.}`

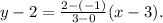
Simplifying the above equation we get:

`y-2=(x-3)\text{.}`

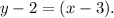
Two points on line m are: (0,4) and (1,2), therefore, its equation is:

`y-4=(4-2)/(0-1)(x-0)\text{.}`

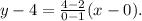
Simplifying the above equation we get:

`y-4=-2x\text{.}`

Since line l is horizontal all its points will have the same y entry y=5, therefore, its equation is:

`y=4.`

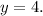
Now, finally, when we have a vertical line its equation will be of the form x=k, where k is the x-entry of the points on the line. Notice that line p is a vertical line, and one point on the line is (-4,0), therefore its equation is:

`x=-4.`

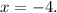
Answer: