Question

Solve the equations. the fractions make it hard for me to understand how to complete it.

Answer 1

x=1131/6424

Explanation:

Given the equation:

`$$(1)/(8)-(5)/(7)\left(x-(5)/(22)\right)=(4 x)/(9)+(1)/(12)$$`

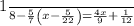
First, open the bracket:

`\begin{gathered} (1)/(8)-(5x)/(7)-(5)/(7)\left(-(5)/(22)\right)=(4 x)/(9)+(1)/(12) \\ (1)/(8)-(5x)/(7)+(25)/(154)=(4x)/(9)+(1)/(12) \end{gathered}`

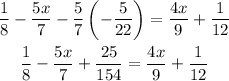
Next, collect like terms:

`\begin{gathered} \text{ Subtract }(1)/(12)\text{ from both sides of the equation} \\ (1)/(8)-(5x)/(7)+(25)/(154)-(1)/(12)=(4x)/(9)+(1)/(12)-(1)/(12) \\ \begin{equation*} (1)/(8)-(5x)/(7)+(25)/(154)-(1)/(12)=(4x)/(9) \end{equation*} \\ \text{ Add }(5x)/(7)\text{ to both sides of the equation} \\ (1)/(8)-(5x)/(7)+(5x)/(7)+(25)/(154)-(1)/(12)=(4x)/(9)+(5x)/(7) \\ (1)/(8)+(25)/(154)-(1)/(12)=(4x)/(9)+(5x)/(7) \end{gathered}`

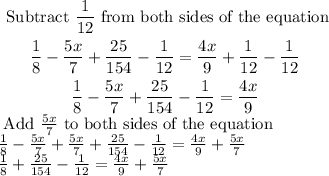
Combine the fractions on the left by finding the LCM of 8, 12, and 154.

The LCM of 8, 12, and 154 = 1848

`\begin{gathered} (231(1)+12(25)-154(1))/(1848)=(4x)/(9)+(5x)/(7) \\ \\ (231+300-154)/(1848)=(4x)/(9)+(5x)/(7) \\ \\ (377)/(1848)=(4x)/(9)+(5x)/(7) \end{gathered}`

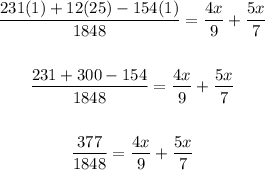
Similarly, combine the fractions on the right by finding the LCM of 9 and 7.

The LCM of 9 and 7 = 63

`\begin{gathered} (377)/(1848)=(7(4x)+9(5x))/(9) \\ \\ (377)/(1848)=(28x+45x)/(63) \\ \\ (377)/(1848)=(73x)/(63) \end{gathered}`

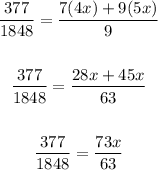
Finally, cross multiply and solve for x:

`\begin{gathered} 73x*1848=377*63 \\ x=(377*63)/(73*1848) \\ \\ x=(23751)/(134904) \\ \\ x=(1131*21)/(6424*21) \\ \\ x=(1131)/(6424) \end{gathered}`

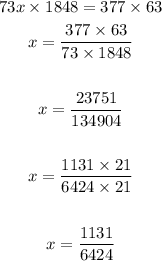
The value of x is 1131/6424.