Question

In a circle with radius 5, an angle intercepts an arc of length 10pi/3. Find the angle inradians to the nearest 10th.

Answer 1

2π/3 rad ≈ 2.1 rad

Step-by-step explanation

The arc length of a portion of a circle with central angle θ and radius r is,

`s=r\cdot\theta`

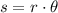
In this case, we know that the arc length is s = 10π/3, the radius is 5, and we have to find the central angle. Solving the equation above for θ,

`\theta=(s)/(r)`

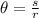
Substitute the known values and solve,

`\theta=((10\pi)/(3))/(5)=(10\pi)/(3\cdot5)=(10\pi)/(15)=(2\pi)/(3)\approx2.1`

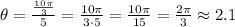
Hence, the angle is 2π/3 radians or 2.1 radians - this last result is rounded to the nearest tenth.