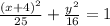Given:
Major axis = 10
Foci at (-1,0) and (-7,0)
Find-: Equation of ellipse.
Sol:
The major axis length is 10.
That mean:
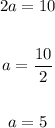
Distance between two foci is:
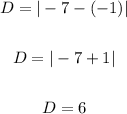
So,

The value of "b" is:

Center of ellipse = Midpoint of foci
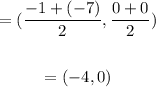
Hence, the equation of the ellipse is: