The area of a triangle is given by
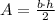
where b is the base and h the height.
If the dimensions are tripled
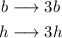
then, the new area will be
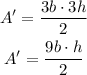
which is equal to
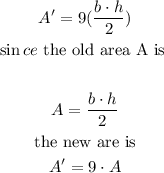
In other words, the new area A' will be 9 times the old area A. Since A is equal to 96 cm^2, we get
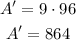
that is, the new area will be 864 cm^2.