First, we need to find the slope of line a, using the next formula

where
(1,-4)=(x1,y1)
(9,-6)=(x2,y2)
we substitute the values

The slope of a perpendicular line to line a is the inverse of the slope we found therefore the slope of line b will be
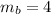
then we will use the slope-point form to find the equation of line b

where
(-6,-24)=(x1,y1)
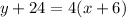
then in order to find the equation in the slope-intercept form, we need to isolate the y
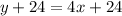

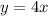
The equation of line b is y=4x