Question

7. P = {1, 2, 3, 4, 5, 6) and Q = {1, 3, 5, 7).(a) Illustrate P and Q on a Venn diagram.(b) List the elements of P U Q. (c) List the elements of Pn Q.

Answer 1

We have two groups of elements, P and Q.

We have to illustrate them on a Venn diagram.

To do that we have to see which elements are common both to P and Q, meaning the elements that are present in both groups.

This elements can be represented as:

`P\cap Q=\mleft\lbrace1,3,5\mright\rbrace`

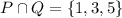
Then, we can draw the Venn diagram as:

In this diagram the elements in P∩Q are present in both groups.

NOTE: P seems to be the list of natural numbers up to 6, while Q is the list of odd natural numbers up to 7. Then, the intersection of both groups ends being the list of odd numbers up to 6.

b) We have to join the two groups and list the elements. The repeated elements, like 1, 3 and 5, are only listed once:

`P\cup Q=\mleft\lbrace1,2,3,4,5,6\mright\rbrace\cup\mleft\lbrace1,3,5,7\mright\rbrace=\mleft\lbrace1,2,3,4,5,6,7\mright\rbrace`

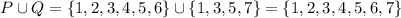
c) We already have written the intersection between P and Q in order to draw the Venn diagram, but we can write it aain:

`P\cap Q=\mleft\lbrace1,2,3,4,5,6\mright\rbrace\cap\mleft\lbrace1,3,5,7\mright\rbrace=\mleft\lbrace1,3,5\mright\rbrace`

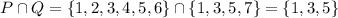
Answer:

a) In the picture

b) {1,2,3,4,5,6,7}

c) {1,3,5}