Question

A party mix is made by adding nuts that sell for $2.50 per kg to a cereal mixture that sells for $1 per kg. How much of each should be added to obtain 80 kg of a mix that will sell for $1.60 per kg?

Answer 1

We have a party mix that constitutes of two items as follows:

`\text{Nuts and Cereal}`

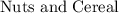
We will assign variables to each item in a party mix. These variables will denote the amount of each item in the party mix as follows:

`\begin{gathered} \text{Nuts: x kg} \\ \text{Cereal: y kg} \end{gathered}`

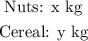
Similarly a price per kg for each item is given to us the problem as follows:

`\begin{gathered} Price(Nuts)=\text{ \$2.5/kg} \\ \text{Price(Cereal) = \$1.00/kg} \end{gathered}`

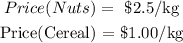
We are given that the net weight of the entire party mix is 80 kg. The party mix constitutes of two items with each respective amounts ( x and y ). We can mathematically express the net weight of the party mix in terms of respective amount of Nuts and Cereal as follows:

`\begin{gathered} Net\text{ weight = Amount Nuts + Amount Cereal } \\ \textcolor{#FF7968}{80}\text{\textcolor{#FF7968}{ = x + y }}\textcolor{#FF7968}{\ldots}\text{\textcolor{#FF7968}{ Eq1}} \end{gathered}`

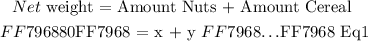
We have expressed the net weight in terms of amount of each item ( x and y ) as Equation 1.

We can also express the value of each item in a pack of party mix. The respective price of each item per kg is given. We can express the value of each item as follows:

`\begin{gathered} \text{Value of Nuts = \$2.5}\cdot x \\ \text{Value of Cereal = \$1.00}\cdot y \end{gathered}`

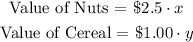
The entire party mix pack is sold for ( $1.60 / kg ). An 80 kg pack of party mix would be sold for:

We can also express the total price of party pack with 80 kg of total mixture by considering the value of each item in that 80 kg pack. We previously determined the value of Nut Cereal in a 80 kg party pack. Hence, we will relate the total price with the respective values of items in the pack as follows:

`\begin{gathered} \text{Total price of party pack = Value of Nuts + Value of Cereal} \\ \textcolor{#FF7968}{128}\text{\textcolor{#FF7968}{ = 2.5}}\textcolor{#FF7968}{\cdot x}\text{\textcolor{#FF7968}{ + y }}\textcolor{#FF7968}{\ldots Eq2} \end{gathered}`

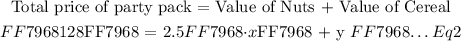
We have two equations. One that relates the amount of Nuts and Cereal in kg in a 80 kg party pack as ( Eq1 ) and the other one relates the Total price of a 80kg party pack in terms of asset value of each item in the pack as ( Eq2 ).

`\begin{gathered} \textcolor{#FF7968}{x}\text{\textcolor{#FF7968}{ + y = 80 }}\textcolor{#FF7968}{\ldots}\text{\textcolor{#FF7968}{ Eq1}} \\ \textcolor{#FF7968}{2.5\cdot x}\text{\textcolor{#FF7968}{ + y = 128 }}\textcolor{#FF7968}{\ldots}\text{\textcolor{#FF7968}{ Eq2}} \end{gathered}`

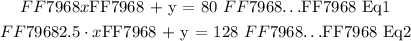
We have two simulataneous equations with two unknowns ( x and y ). We will use the Elimination method to solve the above two equations as follows:

Step 1: Subtract Eq1 from Eq2

`\begin{gathered} -\text{ ( x + y ) = -80} \\ 2.5\cdot x\text{ + y = 128} \\ =========== \\ \textcolor{#FF7968}{1.5\cdot x}\text{\textcolor{#FF7968}{ = 48 }}\textcolor{#FF7968}{\ldots}\text{\textcolor{#FF7968}{ Eq3}} \\ =========== \end{gathered}`

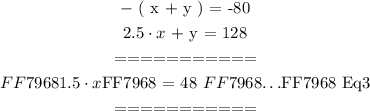
Step 2: Solve for ( x ) using Eq3

`\begin{gathered} x\text{ = }(48)/(1.5) \\ \textcolor{#FF7968}{x=}\text{\textcolor{#FF7968}{ 32 kg}} \end{gathered}`

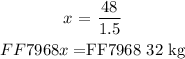
Step 3: Back-substitute the value of ( x ) into Eq1 and solve for ( y ):

`\begin{gathered} 32\text{ + y = 80} \\ \textcolor{#FF7968}{y}\text{\textcolor{#FF7968}{ = 48 kg}} \end{gathered}`

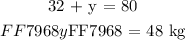
The respective amount of Nuts and cereals in the 80 kg of a mix that will sell for $1.60 / kg is:

`\begin{gathered} \text{\textcolor{#FF7968}{Nuts ( x ) = 32 kg}} \\ \text{\textcolor{#FF7968}{Cereal ( y ) = 48 kg}} \end{gathered}`