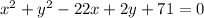Question

Need help with the problem What is the equation of the circle?

Answer 1

Step-by-step explanation

To solve the question, we have to follow the steps below:

Step 1: Get the radius of the circle

To get the radius, we will compare the circumference of the circle with

`2\pi\sqrt[]{51}`

But we know that the circumference of a circle is also obtained by

`2\pi r`

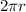
Thus

`\begin{gathered} 2\pi\sqrt[]{51}=2\pi r \\ r=\sqrt[]{51} \end{gathered}`

Step 2: Apply the standard equation of the circle:

`(x-a)^2+(y-b)^2=r^2`

Where

`\begin{gathered} (a,b)\text{ are the center} \\ r=\sqrt[]{51} \end{gathered}`

Step 3: Insert the values to get the equation

`(x-11)^2+(y+1)^2=(\sqrt[]{51})^2`

Simplifying further

`\begin{gathered} x^2-22x+121+y^2+2y+1=51 \\ x^2+y^2-22x+2y+121+1-51=0 \\ x^2+y^2-22x+2y+71=0 \end{gathered}`

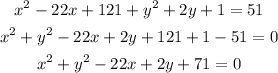
Hence, the equation of the circle will be

`x^2+y^2-22x+2y+71=0`