Question

The exponential model A=883.1e^0.019t describes the population, A, of a country in millions, t years after 2003. Use the model to determine when the population of the country will be 1316 million.The population of the country will be 1315 million in...

Answer 1

Consider the exponential model

`A=883.1e^(0.019t)`

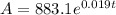
Where A is the population, and t is years after 2003. Then if A= 1315 million, the above equation becomes:

`\text{ 1315 x 10}^6\text{ = }=883.1e^(0.019t)`

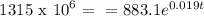
solving for the exponential e, we get:

`\text{ }\frac{\text{ 1315 x 10}^6}{883.1}\text{ }=e^(0.019t)`

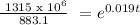
that is:

`e^(0.019t)\text{ =1489072.585}`

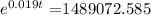
now, applying natural logarithm to both sides of the equation, we obtain:

`ln(e^(0.019t))\text{ =ln(1489072.585)}`

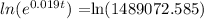
this is equivalent to:

`^{}\text{ 0.019t=ln(1489072.585)}`

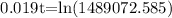
solving for t, we get:

`^{}\text{t=}\frac{\text{ln(1489072.585)}}{\text{ 0.019}}=(14.21)/(0.019)=748.08`

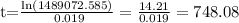
that is, 748.08 years after 2003, that is, in the year:2751.08

So that, the solution is:

The population of the country will be 1316 million in the year 2751.08 or 748.08 years after 2003.