Since the line crosses the x-axis at 15, then
The line passes through the point (15, 0)
The line is perpendicular to the line of the equation
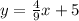
The product of the slopes of the perpendicular lines is -1
So to find the slope of the line that perpendicular to another line,
Reciprocal the slope of the line and change its sign
If the slope of a line is m, then
The slope of its perpendicular is - 1/m
The form of the equation of a line is
y = m x + b
So the slope of the given line is 4/9
Let us find the slope of its perpendicular by reciprocal it and change its sign
The slope of the perpendicular line is -9/4
Substitute it in the form of the equation
y = -9/4 x + b
To find b substitute x and y in the equation by the coordinates of the point (15, 0)
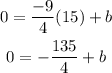
Add 135/4 to both sides to find b

Substitute it in the equation
