1 Answer

Ask a Question

Jroith · Answer 1 · 2023-05-25T03:51:09+0000

ANSWER:

(a) 95.44%

(b) 2.28%

(c) 15.87%

(d) 81.85%

Explanation:

Given:

μ = 66

σ = 4

We must calculate the value of z in each case depending on the values given, we calculate the value of z as follows:

$z=(x-\mu)/(\sigma)$

(a) between 58 and 74.

P (58 < x < 74)

$\begin{gathered} P(58We determine these values with the table, just like this:Therefore:[tex]\begin{gathered} P(z<2)-P(z<-2)=0.9772-0.0228 \\ \\ P(58(b) above 74P (x > 74) [tex]\begin{gathered} P(x>74)=1-P(x<74) \\ \\ P(x\gt74)=1-P\left(z<(74-66)/(4)\right) \\ \\ P(x\gt74)=1-P\left(z<2\right) \\ \\ P(x\gt74)=1-0.9772 \\ \\ P(x\gt74)=0.0228=2.28\% \end{gathered}$

(c) below 62.

P (x < 62)

$\begin{gathered} P(x<62)=P\left(z<(62-66)/(4)\right) \\ \\ P(x<62)=P\left(z<-1\right) \end{gathered}$

We determine this value with the table, like this:

Therefore:

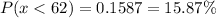
$P(x<62)=0.1587=15.87\%$

(d) between 62 and 74.

P (62 < x < 74)

[tex]\begin{gathered} P(58

Suppose that the scores on a statewide standardized test are normally distributed-example-1

Suppose that the scores on a statewide standardized test are normally distributed-example-2

0 Comments

Please log in or register to add a comment.

Please log in or register to answer this question.

1 Answer

0 Comments

Please log in or register to add a comment.

Other Questions