As the problem can be modeled using a right triangle and the trigonometric functions of the inner angles.
The trigonometric function that relates the two sides of the triangle but not the hypotenuse is the tangent.
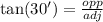
write the tan in function of the information given
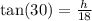
solve the equation for x
![\tan (30)=\frac{\sqrt[]{3}}{3}](https://img.qammunity.org/2023/formulas/mathematics/college/sth06nx9ftxthsynuq9h6l9sq9u6g8b3cc.png)
![\begin{gathered} \frac{\sqrt[]{3}}{3}=(h)/(18) \\ 18\cdot\frac{\sqrt[]{3}}{3}=h \\ 6\sqrt[]{3}=h \\ h=10.392\cong10ft \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/bgsyus290yqqtvbg6royppi40czgpgyzuk.png)