Question

A student fires a cannonball vertically upwards with a speed of 22.0m/s from a height of 40.0m. On the descent, the cannonball misses the building and lands on the ground. Determine all unknowns and answer the following questions. Neglect drag and horizontal motion of the cannonball.What was the cannonball's maximum height (measured from the ground)? With what speed did the cannonball strike the ground? What was the cannonball's total flight time?

Answer 1

We are given that an object is launched with an initial height and we are asked to determine its maximum height. To do that we will determine first the time it takes the object to reach the maximum height which is given by the following formula:

`t=\sqrt[]{(2v_0)/(g)}`

Where:

`\begin{gathered} t=\text{ time for maximum height} \\ v_0=\text{ initial velocity} \\ g=\text{ acceleration of gravity} \end{gathered}`

Replacing the values we get:

`t=\sqrt[]{(2(22(m)/(s)))/(9.8(m)/(s^2))}`

Solving the operations we get:

`t=2.12s`

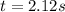
Now, to determine the height associated with this time we will use the following formula:

`h=h_0+v_0t-(1)/(2)gt^2`

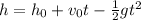
Where:

`h_0=\text{ initial height}`

In this case, the initial height is 40 meters. Replacing the known values:

`h=40m+(22(m)/(s))(2.12s)-(1)/(2)(9.8(m)/(s^2))(2.12s)^2`

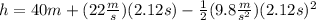
Solving the operations:

`h=64.61m`

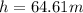
Therefore, the maximum height the ball reaches measured from the ground is 64.61 meters.

Now we are asked to determine the final velocity of the object. To do that, we will use the following formula:

`2gh=v^2_f-v^2_0`

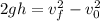
Where:

`\begin{gathered} h=\text{ }initial\text{ height} \\ v_f=\text{ final velocity} \end{gathered}`

Now we solve for the final velocity first by adding the square of the initial velocity:

`2gh+v^2_0=v^2_f`

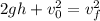
Now we take the square root to both sides:

`√(2gh+v^2_0)=v^{}_f`

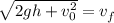
Replacing the known values:

`\sqrt[]{2(9.8(m)/(s^2))(40m)+(22(m)/(s))^2}=v_f`

Solving the operations:

`35.6(m)/(s)=v_f`

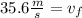
Therefore, the final velocity is 35.6 meters per second directed towards the ground.

Now we are required to determine the time the object stays in the air. To do that we will use the following formula:

`v_f=v_0-gt`

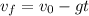
We will solve for "t" first by subtracting the initial velocity from both sides:

`v_f-v_0=-gt`

Now we divide both sides by the acceleration of gravity with the negative sign:

`(v_f-v_0)/(-g)=t`

Now we replace the values, but we need to have into account that since the final velocity is directed towards the ground its sign is negative:

`(-35.6(m)/(s)-22(m)/(s))/(-9.8(m)/(s))=t`

Solving the operations:

`5.87s=t`

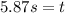
Therefore, the cannonball's total time is 5.87 seconds.