Question

An imported sports car is being carried by plane. The cargo plane is traveling 54 m/s at an altitude of 256 m. The heavy crate containing the car accidentally slips off the back of the plane when it’s directly above your house. How far from your house did it land?

Answer 1

Given,

The initial horizontal velocity of the car, u=54 m/s

The height from which the car was dropped, h=256 m

The initial vertical velocity of the car will be zero.

Thus from the equation of motion, the height from which the car was dropped can be written as

`h=(1)/(2)gt^2`

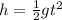
Where g is the acceleration due to gravity and t is the time it takes for the car to reach the ground.

On substituting the known values,

`\begin{gathered} 256=(1)/(2)*9.8* t^2 \\ t=\sqrt[]{(256*2)/(9.8)} \\ =7.23\text{ s} \end{gathered}`

The range of flight of car, i.e., the distance between your house and the point where the car lads is given by,

`R=ut`

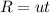
On substituting the known values,

`\begin{gathered} R=54*7.23 \\ =390.42\text{ m} \end{gathered}`

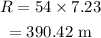
thus the car will land at a distance of 390.42 m away from your house.