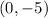Solution
The standard form for the ellipse whose major axis
Write the equation in a standard form
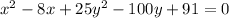

(1) The centre of the ellipse is (h , k)
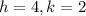
(2) The value of a = 5
(3) The value of b = 1
(4) The foci with the positive x value is the points
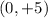
(5) The foci with the negative x value is the points