Question

Determine if the following statement is true or false the relation why equals X squared -6 defines y as a function of X

Answer 1

So we need to tell if the following expression is a function of x:

`y=x^2-6`

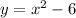
If it is a function then each value of the domain (i.e. each possible x-value) is associated with one and only one value of the range (i.e. any y-value). This basically means that if I choose any x value and use it in the expression then there is only one possible y-value. Now let's assume that for a given x we have two y values: a and b. Then we have two equations:

`\begin{gathered} a=x^2-6 \\ b=x^2-6 \end{gathered}`

In both equations we can add 6 to both sides:

`\begin{gathered} a+6=x^2-6+6 \\ x^2=a+6 \\ b+6=x^2-6+6 \\ x^2=b+6 \end{gathered}`

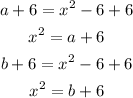
And we can apply a square root to both sides:

`\begin{gathered} \sqrt[]{x^2}=\sqrt[]{a+6} \\ \lvert x\rvert=a+6 \\ \sqrt[]{x^2}=\sqrt[]{b+6} \\ \lvert x\rvert=b+6 \end{gathered}`

So we have to equations for the module of x. We can equalize them:

`\begin{gathered} \lvert x\rvert=\lvert x\rvert \\ a+6=b+6 \end{gathered}`

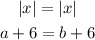
If we substract 6 from both sides we get:

`\begin{gathered} a+6-6=b+6-6 \\ a=b \end{gathered}`

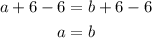
So basically this means that for any x-value there's only one associated y-value. This means that the expression is in deed a function of x so we know the statement is true and the answer is option B.