Question

Suppose your business has a special checking account used just for paying the cable bill. The balance is $800.00 this month. Next month the balance will be $717.50, afterthat it will be $635.00, and on the third month the balance will be $552.50. Which of the following models best illustrates this situation?

Answer 1

The checking account is modeled as a linear function from the data given.

There is a constant decrease every month.

x represents the months

y represents the balance at the end of every month.

`\begin{gathered} P\text{ icking 2 points to get the slope of the function,} \\ (0,800)\text{ and (1,717.5)} \\ \text{where} \\ x_1=0 \\ y_1=800 \\ x_2=1 \\ y_2=717.5 \\ \text{The slope m, is given by} \\ m=(y_2-y_1)/(x_2-x_1) \\ m=(717.5-800)/(1-0) \\ m=(-82.5)/(1) \\ m=-82.5 \end{gathered}`

The slope represents a monthly decrease of $82.5

This shows it is a linear function.

And a linear function is of the form y = mx + C

`\begin{gathered} y=-82.5x+C \\ P\text{ icking a point out to get C,} \\ (0,800) \\ x=0 \\ y=800 \\ y=-82.5x+C \\ 800=-82.5(0)+C \\ 800=0+C \\ C=800 \\ \\ \text{Hence, the equation is;} \\ y=-82.5x+800 \end{gathered}`

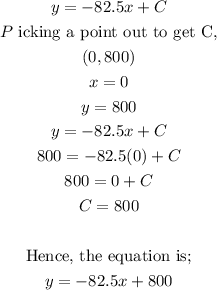
Therefore, the model that best illustrates the situation is y = -82.5x + 800

The correct answer is the third option.