Answer:

Explanations:
The formula for calculating compound amount is expressed according to the formula;
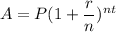
where;
P is the principal (amount saved)
A is the compounded amount
t is the time (in years)
r is the rate (in decimal)
n is the compounding time
Given the following parameters
A = $3738
P = $3000
r = 10.2% = 0.102
n = 12 (compounded monthly)
Substitute the given parameters into the formula to get the required time.
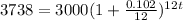
Make "t" the subject of the formula as shown;
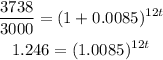
Take the natural logarithm of both sides

This shows that it will take 2.17 years for the account to grow to $3738