Given the equation:
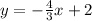
Let's find the equation of the line that is paralle to the given line that passes through (3, 1).
Apply the slope intercept form of a linear equation:
y = mx + b
Where:
m is the slope and b is the y-intercept.
Parallel lines have equal slopes.
Hence, the slope of the line parallel to the given line is:
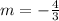
Now, to find the y-intercept(b) of the parallel line, input the point(3, 1) for the values of x and y, and solve for b.
Thus, we have:
Substitute 3 for x, 1 for y, and -4/3 for m

Let's solve for b which is the y-intercept.
We have:

The y-intercept of the parallel line is: y = 5
Therefore, the equation of the line parallel to the given line is:

ANSWER:
