The perimeter of the rectangular garden is 36 feet
The length of the garden is 6 feet less than twice the width.
Let x represent the width of the garden:
w=x
Then we can multiply it by 2 and subtract 6 to determine the length:
l=2x-6
Lets sketch the garden:
The perimeter of a rectangle is the summ of all its sides, that is twice the width plus twice the length:
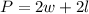
Replace the formula with the given value of P and the expressions for w and l:
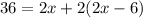
And solve for x, first is to apply the distributive propperty of multiplications to solve the term in parentheses:

The width of the garden is 8 feet
Now calculate the length of the garden:
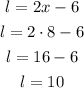
The length of the garden is 10 feet