The function is given as,

( a ) length of the car skid marks = 180 feet.
The speed of the car is calculated as,

Thus the car is traveling at the speed of 60 feet/sec when the skid marks are 180 feet.
(b) length of the car skid marks = 125 feet.
The speed of the car is calculated as,
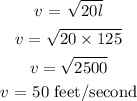
Thus the car is traveling at the speed of 50 feet per second when the skid marks are 125 feet.
( c ) The inverse function is calculated as,
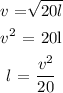
The inverse function gives the value of the length of skid marks when the car has traveled at the speed of v feet per second.