Question

10. Which table shows the same slope as the equation

Answer 1

We are asked which of the following tables have the same slope as the equation

`y=-(5)/(8)x+4`

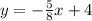
From the equation of a line

`\begin{gathered} y=mx+b \\ \text{where m is the slope and b is the intercept on the y-axis} \end{gathered}`

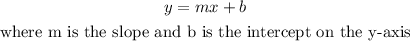
Comparing this to the equation given, we can see that the slope m is

`-(5)/(8)`

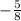
Now, we will use the formula for slope to check which one of the tables has the same slope as that on the equation

`m=(y_1-y_2)/(x_1-x_2)`

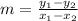
Checking for table F, the slope is

`\begin{gathered} m=\frac{-12-(-4)}{-3-(-1)_{}} \\ =(-12+4)/(-3+1) \\ =(-8)/(-2) \\ =4 \end{gathered}`

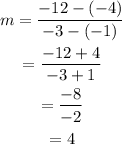
Hence, it is not table F.

Checking for table H, the slope is

`\begin{gathered} m=(6.5-2.75)/(-4-2) \\ =(3.75)/(-6) \\ =-(5)/(8) \end{gathered}`

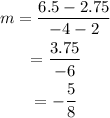
Hence, the answer is table H