Ok so the first thing you should do is take de therm 2x-5 and pass it to the other side of the equation multiplying. After that you can distribute the product like this:
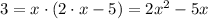
Then you can pass the 3 to the other side so you have a square function equal to 0:
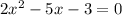
This equation means that you have to look for the roots of a square function. Given a general square function:

Its roots (also named zeroes) are given by:
![x_1,x_2=\frac{-b\pm\sqrt[]{b^2-4\cdot a\cdot c}}{2\cdot a}](https://img.qammunity.org/2023/formulas/mathematics/college/9h8zd74zfz97mc2u4b00ipr3ipmbxfeq8d.png)
In our problem we have a=2, b=-5 and c=-3. Therefore the roots of the square funtion are:
![x_1,x_2=\frac{-(-5)\pm\sqrt[]{(-5)^2-4\cdot2\cdot(-3)}}{2\cdot2}=\frac{5\pm\sqrt[]{25+24}}{4}=(5\pm7)/(4)](https://img.qammunity.org/2023/formulas/mathematics/college/igx4ds4q8xjc6zotulleidxji50urmwbfi.png)
The symbol between 5 and 7 means that one root is calculate by adding and the other by substracting:
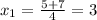

So the roots are 3 and -0.5 and are the two possible values for x. Therefore the correct answer is item A.