The function f(x) = - 4x ^ 3 + 27.24x ^ 2 + 220.4352x - 4.76 is increasing on the open interval

Question

asked May 16, 2023 151k views

1 Answer

Nkosi · Answer 1 · 2023-05-20T13:56:56+0000

Given:

The function is:

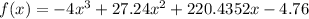
Find:

(a)

The increase in the open interval

(b)

The decrease in the open interval

(c)

The local maximum

Explanation-:

The function is:

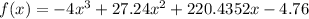
The first derivative of a function is:

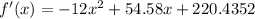
$f^(\prime)(x)=-12x^2+54.58x+220.4352$

For increasing at x

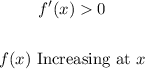
$\begin{gathered} f^(\prime)(x)>0 \\ \\ f(x)\text{ Increasing at }x \end{gathered}$

For decreasing at x

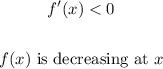
$\begin{gathered} f^(\prime)(x)<0 \\ \\ f(x)\text{ is decreasing at }x \end{gathered}$

f'(x) is zero at a critical point:

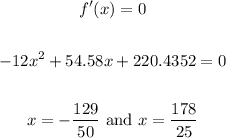
$\begin{gathered} f^(\prime)(x)=0 \\ \\ -12x^2+54.58x+220.4352=0 \\ \\ x=-(129)/(50)\text{ and }x=(178)/(25) \end{gathered}$

So, the interval of increase is:

$\text{ Increasing open interval }=(-(129)/(50),(178)/(25))$

The decreasing interval is all value - increasing interval.

So,

Decreasing interval is:

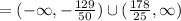
$=(-\infty,-(129)/(50))\cup((178)/(25),\infty)$

The function local maxima is:

The local maxima

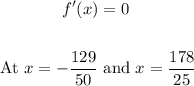
$\begin{gathered} f^(\prime)(x)=0 \\ \\ \text{ At }x=-(129)/(50)\text{ and }x=(178)/(25) \\ \end{gathered}$

For local maxima check the function value:

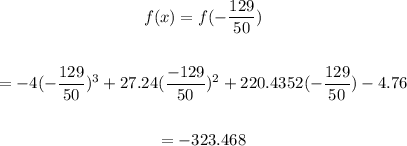
$\begin{gathered} f(x)=f(-(129)/(50)) \\ \\ =-4(-(129)/(50))^3+27.24((-129)/(50))^2+220.4352(-(129)/(50))-4.76 \\ \\ =-323.468 \end{gathered}$

Check the value of another critical point:

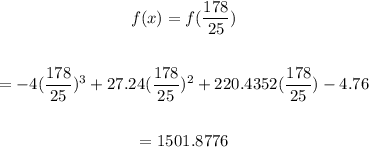
$\begin{gathered} f(x)=f((178)/(25)) \\ \\ =-4((178)/(25))^3+27.24((178)/(25))^2+220.4352((178)/(25))-4.76 \\ \\ =1501.8776 \end{gathered}$

So, the local maxima at

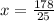
The local maxima is 178/25