Question

How to get the equation of a parabola with 3 pointsy- intercept : (0, -1.4)x-intercept : (0.905,0)3rd point: (2,0.6)

Answer 1

he standard form of a quadratic efunctionis:

`\begin{gathered} y=ax^2+bx+c \\ \text{Where } \\ a,b,\text{ and }c\text{ are real constants such that }a\\e0. \end{gathered}`

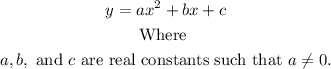
Since the y-intercept is (0, -1.4), it follows that:

`\begin{gathered} -1.4=a(0)^2+b(0)+c \\ \text{ Therefore,} \\ c=-1.4 \end{gathered}`

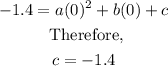
Substitute c = -1.4 into the equation:

`y=ax^2+bx-1.4`

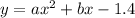
Since the x-intercept is (0.905, 0), it follows that:

`\begin{gathered} a(0.905)^2+b(0.905)-1.4=0 \\ \text{Therefore,} \\ 0.819025a+0.905b=1.4-------(1) \end{gathered}`

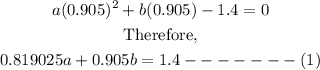
Since the graph passes through the third point (2, 0.6), it follows that:

`\begin{gathered} 0.6=a(2)^2+b(2)-1.4 \\ \text{Therefore} \\ 4a+2b-1.4=0.6 \\ 4a+2b=0.6+1.4_{} \\ 4a+2b=2 \\ \text{Divide both sides by }2 \\ 2a+b=1 \\ \text{Hence} \\ b=1-2a---------(2) \end{gathered}`

Substitute equation (2) into equation (1):

`\begin{gathered} 0.819025a+0.905(1-2a)=1.4 \\ 0.819025a+0.905-1.81a=1.4 \\ \text{ Collect like terms:} \\ 0.819025a-1.81a=1.4-0.905 \\ -0.990975a=0.495 \\ \text{ Therefore,} \\ a=(0.495)/(-0.990975) \\ a\approx-0.5 \end{gathered}`

Substitute a = -0.5 into equation (2), therefore,

`b=1-2(-0.5)=1+1=2`

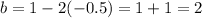
Therfore the function is given by:

`y=-0.5x^2+2x-1.4`

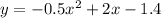
The equation of the parabola is y = -0.5x² + 2x - 1.4

.