Let's use the variables x, y and z to represent each of the three numbers.
If the sum of the three numbers is equal to 80, we have our first equation:
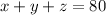
The first number is 8 more than the second, so:
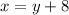
The third number is 2 times the second, so:
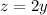
Using these values of z and x in the first equation, let's solve it for y:
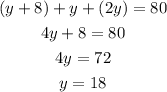
Now, calculating x and z, we have:
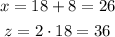
Therefore the first number is 26, the second number is 18 and the third number is 36.