Question

A chemist has a supply of 4.5 liter bottles of a certain solvent that must beshipped to a central warehouse. The warehouse can accept the solvent at a rateof 5 hectoliters per minute for a maximum of 7.5 hours per day. If 1 hectoliterequals 100 liters, what is the maximum number of bottles that the warehousecould receive from the chemist each day?

Answer 1

To solve this question, follow the steps below.

Step 01: Find the maximum volume per day.

The maximum volume per day is when 5 hectoliters per minute are collected for 7.5 hours.

To find this volume, first, let's transform 5 hectoliters per minute into hectoliters per hour.

Knowing that 1 hour = 60 minutes:

`\begin{gathered} 5(hectoliters)/(minute)*(60minutes)/(1hour) \\ 5*60(hectoliters)/(hour) \\ 300(hectol\imaginaryI ters)/(hour) \end{gathered}`

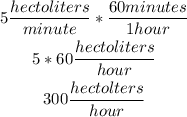
Now, let's multiply by 7.5 hours to find how many hectoliters are collected per day:

`7.5*300=2250(hectoliters)/(day)`

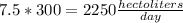
Step 02: Transform the volume to liters.

Since 1 hectoliter = 100 liters.

`\begin{gathered} 2250(hectoliters)/(day)*100(liters)/(hectoliter) \\ 225000(l\imaginaryI ters)/(day) \end{gathered}`

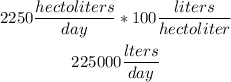
Step 03: Find the number of bottles.

Since 1 bottle has 4.5 liters:

`\begin{gathered} 225000(l\imaginaryI ters)/(day)*\frac{1\text{ }bottle}{4.5\text{ }litters} \\ (225000)/(4.5)(bottles)/(day) \\ 50000(bottles)/(day) \end{gathered}`

Answer: The maximum number of bottles the warehouse can receive in one day is 50,000.