Question

In the circle below, segment AB is a diameter. if the length of are ACB is 6, what is the length of the radius of the circle?

Answer 1

If AB is the diameter, it means the arc ACB is a semicircle (arc of 180°).

So, to calculate the radius of the circle, we can use the following rule of three:

`\begin{gathered} \text{arc}\to\text{length} \\ 360\degree\to2\pi r \\ 180\degree\to x \\ (360)/(180)=(2\pi r)/(x) \\ 2=(2\pi r)/(x) \\ 2x=2\pi r \\ x=\pi r \end{gathered}`

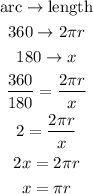
The length of a semicircle is given by πr. If this arc measures 6π, we have:

`\begin{gathered} \pi r=6\pi \\ (\pi r)/(\pi)=(6\pi)/(\pi) \\ r=6 \end{gathered}`

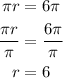
So the radius of this circle is equal 6 units.