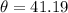Question

Find the angle of elevation of the sun from the ground when a tree that is 14ft tall casts a shadow 16ft long. Round to the nearest degrees

Answer 1

Question:

Find the angle of elevation of the sun from the ground when a tree that is 14ft tall casts a shadow 16ft long. Round to the nearest degrees.

Solution:

Consider the following diagram of the problem:

Applying the appropriate trigonometric identity to the right triangle in the diagram, we obtain:

`\tan (\theta)=\text{ }(14)/(16)`

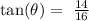
now, applying to both sides of the equation the inverse function of the tangent, we get:

`\tan ^(-1)(\tan (\theta))=\text{ }\tan ^(-1)((14)/(16))`

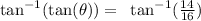
this is equivalent to:

`\theta=tan^(-1)((14)/(16))=\text{ 41.185}\approx41.19`

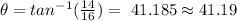
then, the correct answer is:

`\theta=41.19`