Question

TVLI9ia Exercises 11.8 Complete the following: Find the distance between the line and the point. (a) 3r + 4y = 24; (-10, 1) (c) x + 2y = 12; (4, -6) (e) r + 3y = 0: (1-77. (b) 7x - 6y = -32; (5,-3) (d) x + y = -4; (-1, 7) (f) y = 3; (3, -3) Fxam

Answer 1

If a line is written in the form:

`ax+by+c=0`

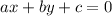
And the coordinates of a point are:

`(x_0,y_0)`

Then, the distance between the line and those points, is:

`d=\frac{\lvert ax_0+by_0+c\rvert}{\sqrt[]{a^2+b^2}}`

a)

`3x+4y=24;(-10,1)`

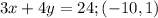
First, rewrite the equation in general form setting it equal to 0 by substracting 24 from each side:

`\begin{gathered} 3x+4y=24 \\ \Rightarrow3x+4y-24=0 \end{gathered}`

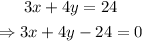
Comparing this equation to the general form of a line, we know that:

`\begin{gathered} a=3 \\ b=4 \\ c=-24 \end{gathered}`

Substitute those values and the coordinates (-10,1) into the line-point distance formula:

`\begin{gathered} d=\frac{\lvert3(-10)+4(1)-24\rvert}{\sqrt[]{3^2+4^2}} \\ =\frac{\lvert-30+4-24\rvert}{\sqrt[]{9+16}} \\ =\frac{\lvert-50\rvert}{\sqrt[]{25}} \\ =(50)/(5) \\ =10 \end{gathered}`

Then, the distance between the given line and the given point in part a), is 10.

Apply a similar procedure to find all other distances.