Question

*QUESTION ATTACHED*Answer choices 1. The graph has a relative minimum2The graph of the quadratic function has a vertex at(0,5)3. The graph opens up 4. The graph has one x intercept 5. The graph has a y- intercept at (5,0)6. The axis of symmetry is approximately =0Select all that apply

Answer 1

Given

The table which represents a quadratic equation is,a

To find the options which are true for the quadratic equation.

Step-by-step explanation:

It is given that,

Then, the quadratic equation is of the form,

`y=ax^2+bx+c`

Put x=0 and y=5 in the above equation.

That implies,

`\begin{gathered} 5=a(0)^2+b(0)+c \\ 5=c \end{gathered}`

Then, the quadratic equation becomes,

`y=ax^2+bx+5`

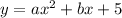
Put x=-1, y=7 and x=1, y=7 in the above equation.

That implies,

`\begin{gathered} 7=a(-1)^2+b(-1)+5 \\ 7=a-b+5\text{ \_\_\_\_\_\_\_\_\lparen1\rparen} \\ 7=a(1)^2+b(1)+5 \\ 7=a+b+5\text{ \_\_\_\_\_\_\_\lparen2\rparen} \end{gathered}`

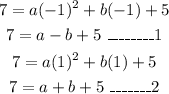
Adding (1) and (2) implies,

`\begin{gathered} 2a+10=14 \\ 2a=14-10 \\ 2a=4 \\ a=(4)/(2) \\ a=2 \end{gathered}`

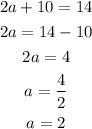
And,

`\begin{gathered} 7=2-b+5 \\ 7=-b+7 \\ b=0 \end{gathered}`

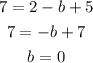
Hence, the quadratic equation is,

`y=2x^2+5`

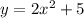
Now,

That implies,

The graph is opened up and the graph has one x-intercept.