hello
to solve this problem, we would simply use the formula of compound interest
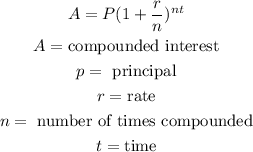
from this, we can write out our data and then substitute it into the formula
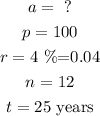
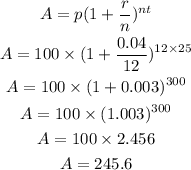
in 25 years, i will have the sum of $245.6 after compounding $100 monthly at 4% interest rate