Given:
a.) A circle has a radius of 20 cm.
b.) It has a central angle that measures 216 degrees.
Let's draw the figure to better understand the scenario:
For us to be able to determine the arc length, we will be using the following formula:
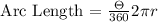
Where,
r = radius of the circle
Θ = central angle
We get,
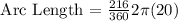
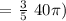
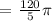
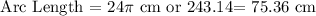
Therefore, the length of the arc is 24π cm or 75.36 cm