Question

The access code of a garage door consists of three digits. Each digit can be any number from 1 through 8, and each number can be repeated. 1. Find the number if possible access codes. 2. What is the probability of randomly selecting the correct access code on the first try? 3. What is the probability of not selecting the correct access code on the first try? Round to three decimal places on 2 and 3

Answer 1

Given that each number can be repeated, we use the following formula to find the number of possible codes.

`n^m`

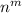
Where n = 8 (the total number of digits) and m = 3 (the number of digits needed for a code).

`8^3=512`

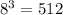
(1) Therefore, there are 512 possible access codes.

In order to find the probability of randomly selecting the correct access code is 1/512 because there's just one correct code among 512 total.

`P_{\text{correct}}=(1)/(512)\approx0.002`

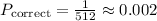
(2) Therefore, the probability of randomly selecting the correct access code is 0.002.

At last, to find the probability of not selecting the correct code, we just have to find the complement probability, which consists in subtracting from 1.

`P_{\text{not correct}}=1-(1)/(512)\approx0.998`

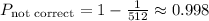
(3) Therefore, the probability of not selecting the correct access code is 0.998.