Question

Solve the quadratic by completing the square x^2-4x-9=0

Answer 1

We are given the following quadratic equation

`x^2-4x-9=0`

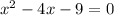
When we have a quadratic equation of the form:

`x^2+bx+c=0`

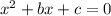
Then, to complete the square we add and subtract the following expression:

`((b)/(2))^2`

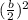
Replacing the value of "b"

`((4)/(2))^2=2^2=4`

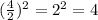
Adding and subtracting the term:

`x^2-4x+4-4-9`

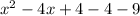
Associating terms:

`(x^2-4x+4)+(-4-9)=0`

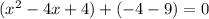
factoring the expression in the first parenthesis:

`(x-2)^2+(-4-9)=0`

Solving the operation in the second parenthesis:

`(x-2)^2-13=0`

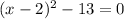
Now we solve for "x", first by adding 13 to both sides:

`\begin{gathered} (x-2)^2-13+13=13 \\ (x-2)^2=13 \end{gathered}`

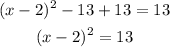
Now, we take square root on both sides:

`x-2=\sqrt[]{13}`

Now we add 2 to both sides:

`x=2\pm\sqrt[]{13}`

We have to possible values for "x", the first value is:

`x=2+\sqrt[]{13}=5.6`

The second value is:

`x=2-\sqrt[]{13}=-1.6`