Given a polynomial function:
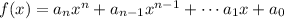
We call the term a_n as 'leading coefficient ' and the n in x_n as the degree of the function
In the case of the figure, we can notice that the graph of the function intercepts the x-axis in 5 points, this means (after supposing that the function is indeed a polynomial one) that the degree of the function is 5 (n=5)
In general, checking how many times the graph of a function intercepts the x-axis is the easiest way to find out its degree.
As for the leading coefficient, notice that for x>0 and x very large, we get that f(x)>0. When the value of x is large, the term x^5 'dominates' the other 5 terms (a_4x^4,a_3x^3, etc.).
So, we get:
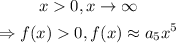
So, as x >0 and f(x)>0, a_5 has to be greater than zero, a positive number.
The leading term is a positive number